その予測、必要ですか？~意思決定分析と予測の活用を読んで~

この記事は？

企業のDXを支援するコンサル会社に勤めてきた中で、予測モデルを作る経験をしてきました。二値分類モデルならconfusion matrixをもとにモデルを評価するのが一般的でしょうが、結局、案件の状況で正解率や適合率などに見る指標を変えてるなあと思っていました。ある時、この本に出会い、「モデルの価値は意思決定問題によって変わる」ということが明確に理解できました。意思決定支援のためにデータ分析する人は全員読んだ読んだほうがいい本です。個人的にとても感動したので、共有するために書きます。

二値分類モデルの良さってconfusion matrixなの？

一般的に二値分類モデルの性能はconfusion matrixで評価することが推奨されています。しかし、これには問題があると筆者は考えます。

  1. confusion matrixは予測の確からしさを測ると解釈できますが、そもそも予測を得ること自体に価値はない。予測を得ることで意思決定が向上することで初めて価値が生まれると考えます。天気予報を見て傘を持っていくかどうかをの判断することができれば、天気予報に意味はありますが、折り畳み傘をいつも持ち歩くと決めているなら天気予報に意味はないですよね。
  2. 意思決定をどれくらい良くするかがconfution matrixのみでは決まらない。例を挙げます。まったく同じconfusion matrixを持つ二値分類モデルがあります。ただし、虚報は少ないようですが、見逃しが多いようです。つまり、適合率は高いですが、再現率が低いようです*1。次の二つの意思決定問題を考えてみます。
    ①工場の検査工程の不良品検査を二値分類モデルで代替し、省人化したい。不良品を出荷してしまうと顧客の信頼を完全に失うことになる。
    ➁工場の検査工程の不良品検査を二値分類モデルで代替し、省人化したい。不良品を出荷したとしても、顧客はその前提で商品を購入している。
    前者では見逃しが許されず、後者では見逃しはある程度許容できそうです。よって、省人化のメリットが同量だとして、➁ではそのメリットが十分なら受け入れられそうですが、①の案件では受け入れられないでしょう。同じconfusion matrixを持つモデルでも意思決定問題によってその価値が変わることがわかります。

つまり、予測の価値は意思決定問題と分離して考えることはできないです。よって、意思決定の営み自体をモデル化し、その中で予測が生む価値を考えていきます。

意思決定のモデル化

意思決定本を参考にして、次のような意思決定の問題を考えてみます。

あなたはある工場のマネージャーです。工場では月の終わりに、来月稼働する生産機械の数を調整することができます。稼働する生産機械が多ければたくさん製品が作れますが、すべて売れるとは限りません。製品の需要は景気によって左右されることがわかっています。利益を最大化するために、来月何台稼働させれば良いかというのが問題です。

問題の構成要素

天下り的ですが、意思決定モデルの構成要素を紹介します。

行動 A

これはどの選択肢を選ぶかということを意味します。例えば、傘を持っていくかどうかという意思決定問題の行動は、「傘をもっていく」と「傘をもっていかない」の2つです。

自然の状態 \theta

行動の価値は、自然の状態によって変化します。例えば、自然の状態が「雨」「晴れ」の二種類あったときに、「傘をもっていく」という行動の価値は異なります。また、それぞれの自然の状態の確率も考えることができるでしょう。

利得 c(A, \theta)

ある自然の状態における行動の価値です。例えば、自然の状態が「雨」「晴れ」、行動が「傘をもっていく」「傘をもっていかない」の時に、利得の行列は、

傘をもっていく 傘をもっていかない
雨 濡れなくてうれしい！ 濡れて辛い
晴れ 無駄な荷物だった 手ぶらで楽

というように表せます。

今回の問題において

さて、今回の意思決定問題におけるこれらの要素を明確にしていきましょう。

  • 行動は、稼働台数が自然数ならば何でも良さそうですが、簡単のため、「1台稼働させる」「2台稼働させる」にします。それぞれ a_1, a_2と表します。

  • 自然の状態は景気について考えることにします。簡単のため、「好景気である」「不景気である」にします。それぞれ \theta_1, \theta_2と表します。また、過去のデータの調査から P(\theta_1) = 0.4, P(\theta_2) = 0.6ということがわかっています。これは、現場の主観的な確率ということにします*2。

  • 利得行列を考えましょう。今回は、好景気では2台稼働させるとたくさん作れてたくさん売れてめっちゃ儲かりますが、不景気に2台稼働させると製品が売れず余ってしまうので、稼働費用の分だけマイナスになるとします。1台稼働させる場合は、量は作れないので儲けはそこそこですが、不景気でも売り切れるとします。これを数値化して利得行列を表します*3。

2台稼働させる a_1 1台稼働させる a_2
好景気 \theta_1 700 300
不景気 \theta_2 -300 300

そもそも、予測する価値はあるのか？どれくらい予測することにコストをかけるのか？

「来月の景気が予測できれば、最適な稼働台数が決められるのになあ」とだれかが言いました。「そうだ！AIに予測させよう！」  
ということで来月の景気をAIに予測させて、それをもとに稼働台数を決めるプロジェクトが走ることになりました。

まあ、やりたいことはわかります。でも少し落ち着いてください。現時点でも、現場の感覚として来月の景気は多少予測できます。現時点での意思決定の良さを確認しましょう。また、最強のAIが出来たとしたら、来月の景気は必ず当てることはできますが、そのときの意思決定は現在と比べてどれくらい良くなるでしょうか。それがわかれば、このプロジェクトにどれだけ予算をかけていいかざっくりわかるはずです。

決定木分析

まずは、今回の意思決定問題がどんなものかわかりやすくするために可視化してみましょう。決定木という手法を用いると、今回の意思決定問題は次の図のように表せます。

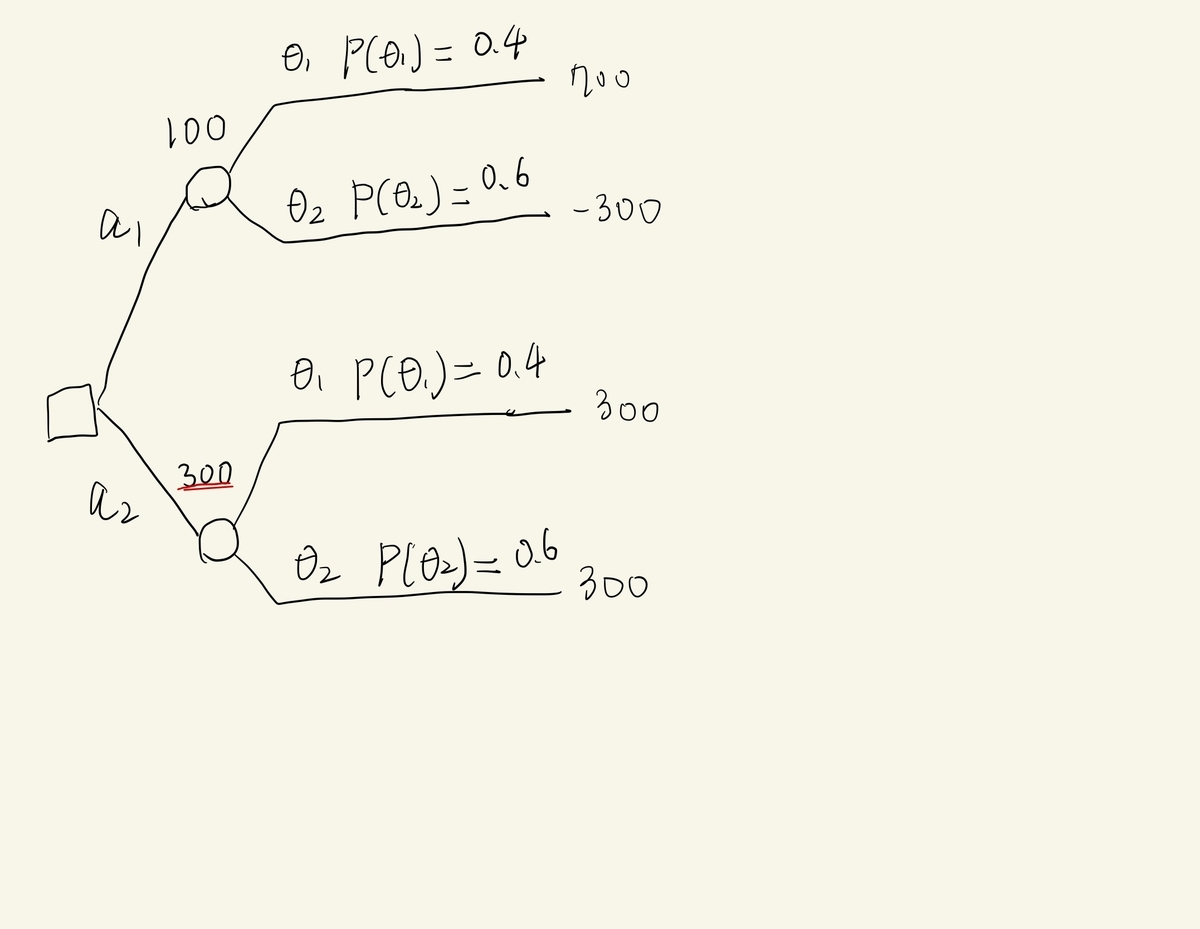
f:id:wata101wata:20210328205413j:plain
予測なしの意思決定問題
説明をしていくと、□を決定ノードと呼び、ここで行動を選択します。〇をチャンスノードと呼び、自然の状態が決まります。利得が先端に書かれています。 この時、□で a_1を選ぶことはどのくらい良いでしょうか。それは、 a_1を選んだときの、利得の期待値で表すことが素直でしょう。これをEMV (Expected Monetary Value)とよび、 P(\theta)が与えられたときa_1をした時のEMVをEMV(a_1|P(\theta))と表します。各決定ノードの上にこれを書いてあります。今回の意思決定問題のときでは、
\displaystyle EMV(a_1|P(\theta)) = P(\theta_1)*c(a_1, \theta) + P(\theta_2) * c(a_1, \theta_2)
\displaystyle = 0.4 * 700 + 0.6 * -300
\displaystyle = 100
となります。

予測なしで意思決定

予測なしの意思決定の価値は、予測なしで EMVを最大化するように意思決定したときの EMVでしょう。よって、予測なしの意思決定の価値 V_{nopred}は、
\displaystyle V_{nopred} = EMV(a_2|P(\theta)) = 300
となります。

完全情報による意思決定

完全情報とは、今回の意思決定問題では、来月の景気を絶対に当てることができるということです。 \theta_1なら a_1を選び、 \theta_2なら a_2を選ぶので、そのときの意思決定の価値 V_{perfect}は、
\displaystyle V_{perfect} = P(\theta_1) * 700 + P(\theta_2) * 300 = 480

予測AIプロジェクトの実施可否への考察

上記の計算から、予測によって生み出すことのできる価値の最大量は、 \displaystyle V_{perfect} - V_{nopred} = 480 - 300 = 180
となります。よって、このプロジェクトで得られる価値は最大でも180万円ですから、それがまず目安となるでしょう。

意思決定モデルの下での二値分類モデルの価値

ここからは、予測が得られるとして考えていきます。

予測がある場合の 問題の構成要素

予測がない場合の構成要素に加えて、以下の要素を考えます。

予測 F

行動をとる前に得られるとします。今回の場合は、「来月が好景気である f_1」、「来月が不景気である f_2」のどちらかであるとします。

ある二値分類モデルの価値

まずは、二値分類モデルの性能を与えます。confusion matrixが次であったとしましょう。

好景気予測 f_1 不景気予測 f_2
好景気 \theta_1 P(\theta_1, f_1) = 0.35 P(\theta_1, f_2) = 0.05
不景気 \theta_2 P(\theta_2, f_1) = 0.10 P(\theta_2, f_2) = 0.50

好景気をpositiveと考えて、正解率85%、再現率は87.5%、適合率は77.8%のモデルです。このモデルの予測が与えられたときの意思決定問題を考えてみます。これも決定木で表してみます。

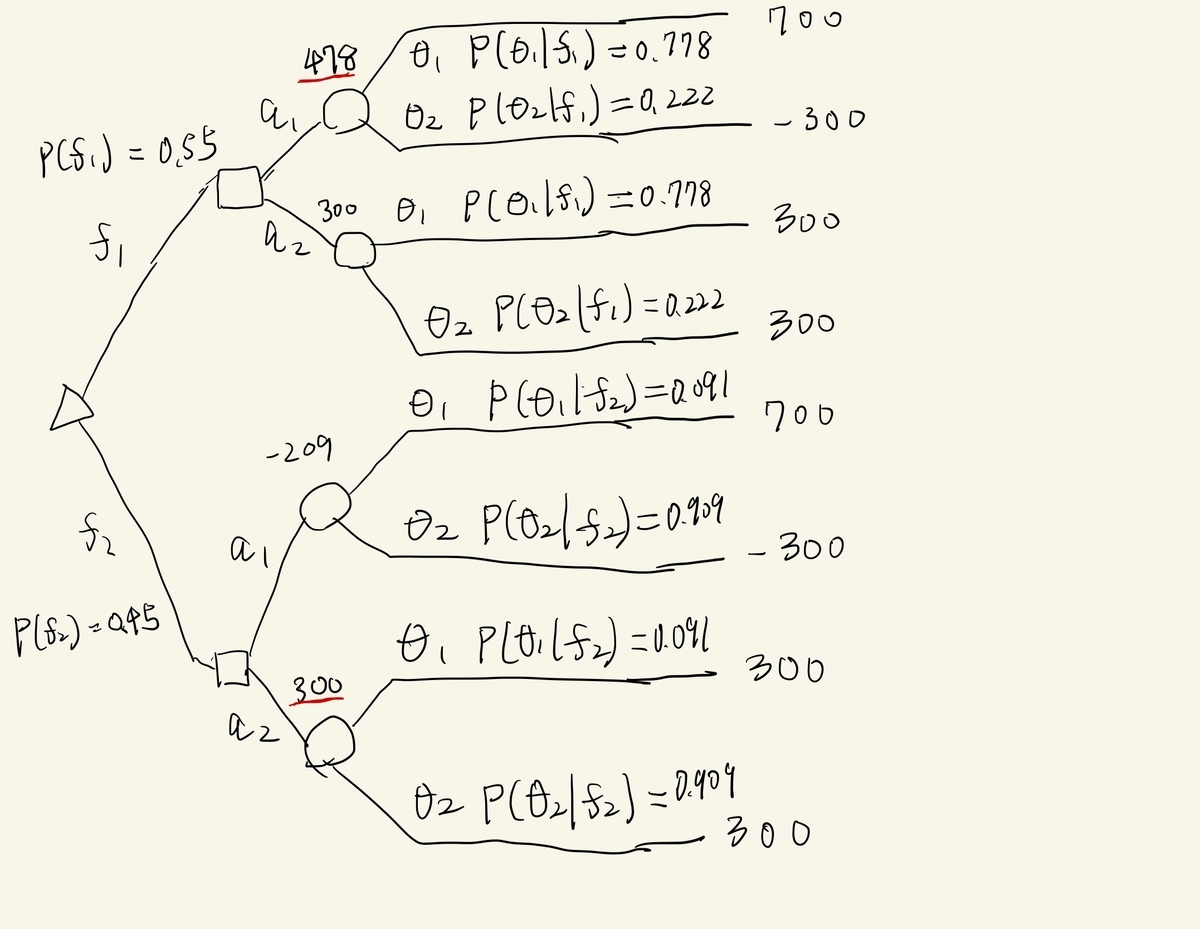
f:id:wata101wata:20210328205439j:plain
予測ありの意思決定問題
△は予測が与えられる予測ノードです*4。このノード以降の確率は予測で条件付けられた確率を計算してください。例えば、予測 f_1の下で、行動 a_1を取るときの期待利得は、 \displaystyle EMV(a_1|P(\theta|f_1)) = P(\theta_1|f_1) * c(\theta_1, a_1) + P(\theta_2|f_1) * c(\theta_2, a_1)
\displaystyle = 0.778 * 700 + 0.222 * -300 = 478
となります。ですから、 f_1の時は a_1、f_2の時は a_2を選ぶので、予測があるときの意思決定の価値 V_{predict}は、 \displaystyle V_{predict} = P(f_1) * EMV(a_1|P(\theta|f_1)) + P(f_2) * EMV(a_2|P(\theta|f_2))
\displaystyle = 0.45 * 478 + 0.55 * 300 = 380
となります。この結果からこの予測モデルは80万円の価値があったことがわかりました*5。

まとめ

ここまで読んでいただいた方は、まずは参考にした意思決定分析と予測の活用を読んでください。

自然の状態が2つの意思決定問題について二値予測モデルの価値を測ることができました。今後さらに勉強していきたい内容を述べます。何か知っている方がいたら教えてください。

  • モデルの拡張。単純にマルチクラスにするとどうなるのでしょう。線形回帰して顧客をスコアリングし、それをもとに意思決定する場合はどのように考えればいいのでしょう。

  • 因果推論との関連性。因果性をもとに意思決定する場合も現実世界ではあると思うのですが、その場合も今回と同じように考えてもいいのですかね？つまり、 aを投薬の有無にして、 \thetaをその後の病気の有無にするとかです。ダメな気がしますね。RCTとかして、因果であると言い切れるような場合ならやって良いかもしれません。

  • ベイズ統計との関連性。 P(\theta)ってベイズ統計でいう主観確率っぽい印象を受けるのですが、よくわかりません！ここは全く分からないときは一様分布にしてしまっていいのでしょうか。

*1:https://www.atmarkit.co.jp/ait/articles/2010/27/news020.html#binaryaccuracy

*2:後述する予測AIを作るプロジェクトが走る前の、簡易なデータ分析の結果と考えても良いでしょう

*3:ここの数値化は、現実では現場へのヒアリングや実績の調査をするのでしょう。

*4:これは私だけの定義なので注意してください

*5:ここ感動ポイント